χ(カイ)です。医療従事者として病院に勤務しながら研究を行っています。研究初心者がわかりやすいと思ってもらえるような内容のブログを書いています。
サンプルサイズって?
サンプルサイズを設定しないと研究はできないのか?
サンプルサイズが適切でないと統計分析を行うことはできないのか?
そもそもサンプルサイズを事前に設定することは必要なのか?
これらの疑問は感じる方が多いのではないのでしょうか。
ここでは、最低限知っておくべき知識でサンプルサイズを計算することに関して解説していきます。
目次
サンプルサイズとサンプル数の用語について
サンプルサイズ(sample size、標本サイズ、標本の大きさ)とサンプル数(the number of samples、 標本数)を間違えて使用している人は多いのではないでしょうか。
私自身も良く間違えてました。
この用語が一緒になってしまっている人が多いと思いましたので、ここで簡単に説明します。
例)
23人と27人のBMIの平均の差を検定する場合、サンプル数は2であり、サンプルサイズは23と27となる。
ということは、群数と呼ばれるのがサンプル数であり、n数と呼ばれる数値の方がサンプルサイズですね。
サンプルサイズの計算は必要か?
そもそも研究をする前にサンプルサイズを設定しておくことは必要なのでしょうか?
私も計算して方が良いのかわからず、計算しなくても良いのではないかと思っていました。
しかし、統計には以下の特徴があるのです。
サンプルサイズが多ければ多いほど解析の精度が上がり、それに伴いp値は小さくなる。極端に言えば、臨床的に意味のないどんなに小さな差でも、サンプルサイズを増やせばいつかは統計的には有意となる。
そのため、サンプルサイズ(n数)が多ければ良いわけではなく、適切なサンプルサイズで差があることを示す必要があります。
実際には下の表のように示されていることを参考にすることもあります。
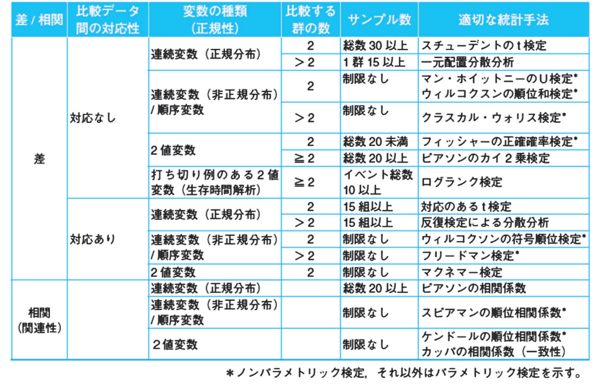
サンプルサイズが大きいとp値は小さくなる
本当に2群間に差があって有意差が出る場合もあれば、サンプルサイズが大きいために有意差が出るといった場合があります。
したがって適切なサンプルサイズで統計学的な検定を行わないと、サンプルサイズが大きかったから有意差が出たということになってしまいます。
そのため、通常は事前に必要なサンプルサイズを決定してから研究を行うことが必要です。
サンプルサイズによる違い(実際)
以下は実際にデータを使用し、SPSSにて解析した結果を示しています。
①n=18 サンプルサイズ小
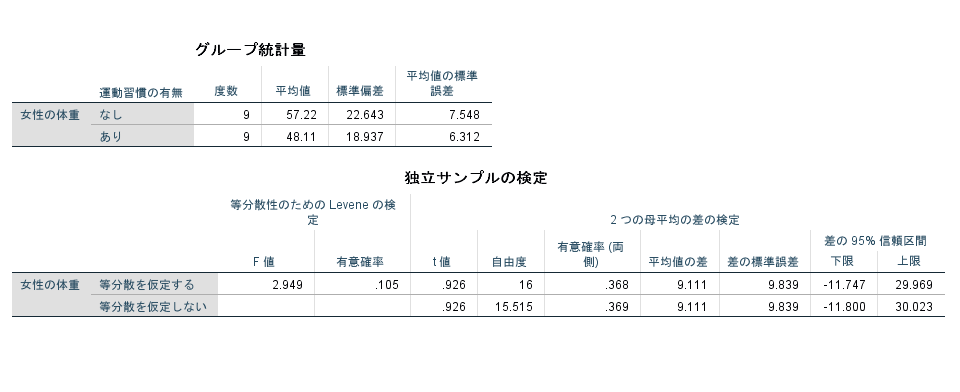
②n=600 サンプルサイズ大
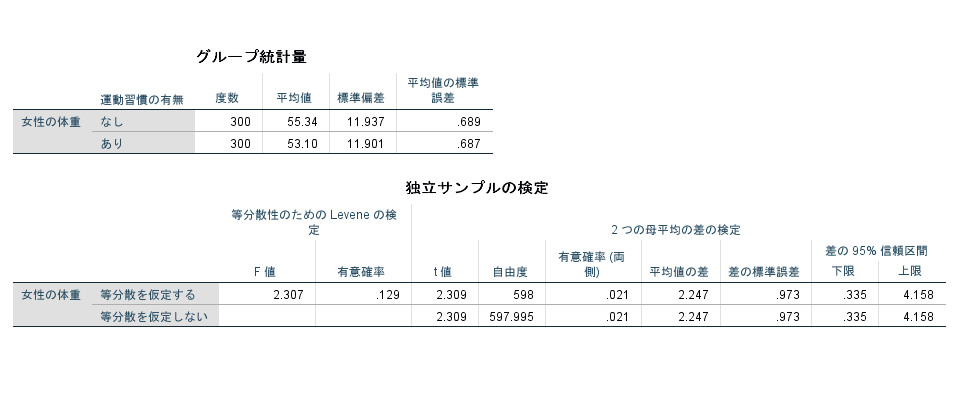
この2つの結果から平均値だけを確認すると(標準偏差を考慮せずに)、
n=600の場合に比べてn=18の場合の方が、
運動習慣がある方が体重が軽いと数値上は感じると思います。
サンプルサイズの小さい方が差が大きいね
しかし、有意確率(両側)の部分では、
サンプルサイズの大きい(n=600)の
数値上の差が少ない方が
有意に差がある(0.05より小さい)
という結果になっています。
この結果からみてもサンプルサイズが大きい方が、実際の差がどうかというよりも統計学的に有意になりやすいことが確認できると思います。
サンプルサイズを計算するためのフリーソフト
私が実際に使用しているのが、「G*power」というフリーソフトです。
その他に「R」でも計算できるようですが、私はこちらで計算しています。
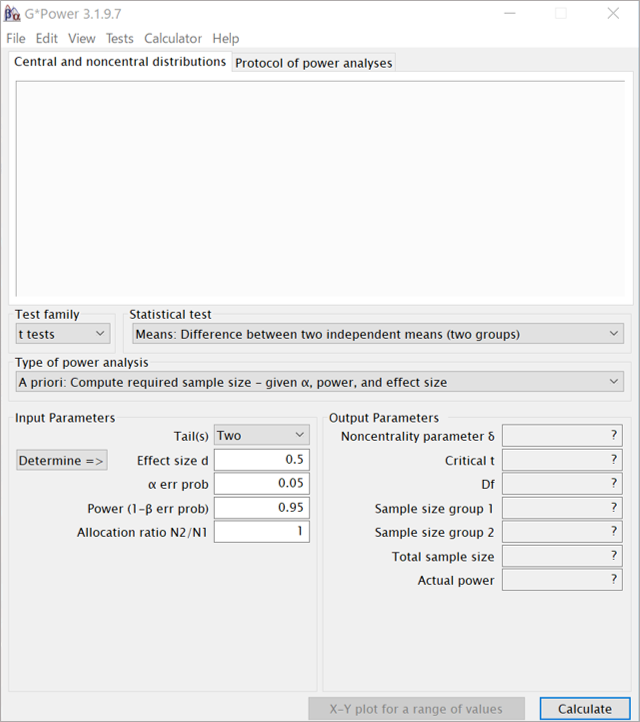
G*powerの画面
「G*power」は様々なテストのサンプルサイズを計算することができます。
下の画面は実際のソフトを開いたときの画面です。
全て英語表示ですが、慣れてしまえば問題ないと思います。
日本語で詳しく解説された文書があり、私も参考にさせていただいています。
水本篤, 竹本理: 効果量と検定力分析入門―統計的検定を正しく使うために―, 外国語教育メディア学会 (LET) 関西支部 メソドロジー研究部会 2010 年度報告論集, pp47–73, 2010
G*powerを使う前にまず押さえておく知識
「G*power」でサンプルサイズを計算する前に事前に押さえておく知識があります。
それが、以下の図の4つの用語です。
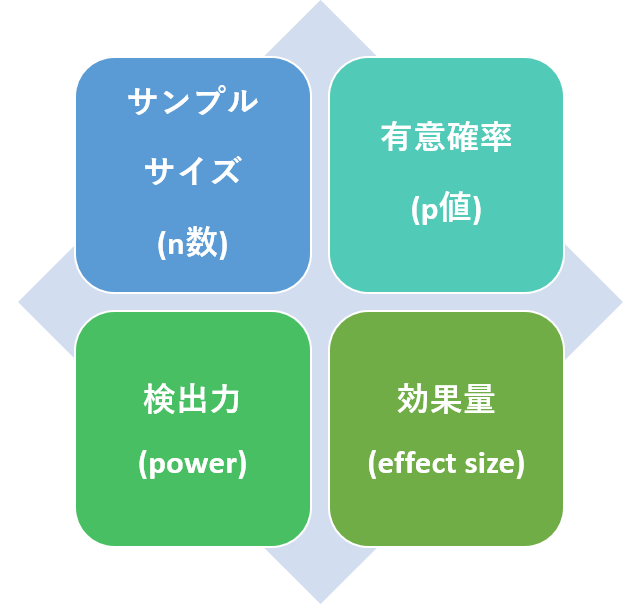
サンプルサイズを計算するために、その他の3つが決まればサンプルサイズが決まってきます。
有意確率(αエラーを起こす確率)
αエラーは1型エラー(第1種過誤) とも言います。
ここでもまた聞きなれない言葉が出てきましたね。
1型エラー(第1種過誤):本当は差がないのに、「差がある」と誤ってしまうこと
2型エラー(第2種過誤):本当は差があるのに、「差がない」と誤ってしまうこと
有意水準 = α = 1型エラー = 第1種過誤
ここで数値として表すには、有意水準で良く用いられる、「0.05(5%)」や「0.01(1%)」となります。
有意水準が5%より外れるということは、差がない場合、5%の確率(100回のうち5回発生)で発生することが起こったということです。
検出力(power)
検出力とは、本当に差がある薬があって、正しく効果があると言える力のことです。
検出力(Power)は、「1ーβ」で表します。
これは、2型エラー(第2種過誤)の逆ですね。
「本当に差があるときに正しく差がある」と判断する確率です。
検出力は慣習的に0.8くらいが望ましい(100人のうち80人に差がある効果がある、最低80%)と言われています。
症例数を増やすと検出力は高くなるため、90%を超えるのは症例数が多すぎると言われるようです。
検出力が大きいほどp値は小さくなります。
効果量(effect size)
効果量は差の実際の程度を表します。
変数間の関係の強さを表します(相関係数、回帰分析における決定係数など)。
効果量はサンプルサイズの影響を受けません。