統計学の本を読むと必ず最初の方に出現する用語である「正規分布」
正規分布と聞いて、その部分の説明を飛ばしたり、その時点で統計学を学ぶことを諦めてしまったりする方は多いと思います。
私もその1人でした。
しばらくは十分な理解をせずに飛ばしてました。
今回は正規分布を理解するために必要な内容をまとめてみました。
正規分布とは?
- 集めたデータのばらつきが、平均値を境にして前後に同じくらいばらついている状態のこと
- 英語ではnormal distribution ⇒ 「ふつうの広がり」
こんな感じの左右対称の曲線です
正規分布の特徴
- 自然現象や社会現象(人間の行動や性質など)には、正規分布に従うものが多くある
- 長さ、重さ等の計量値は全て正規分布している
- だいたいが、大きくてもこれくらい、小さくてもこれくらいというちょうどいい範囲を特定できる
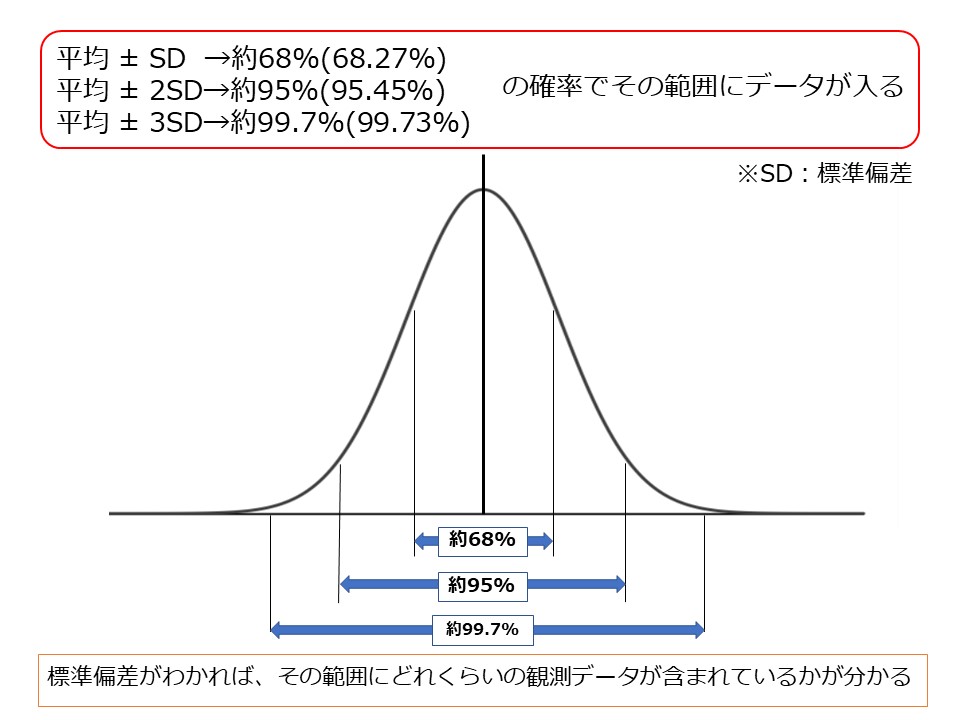
分布の形は平均と標準偏差で決まります
平均は中央の場所、標準偏差は分布の幅を決めます
収集したデータが正規分布していれば以下の図のように
その範囲にどのくらいのデータがあるのかわかります
分布の客観的な判断は難しい…
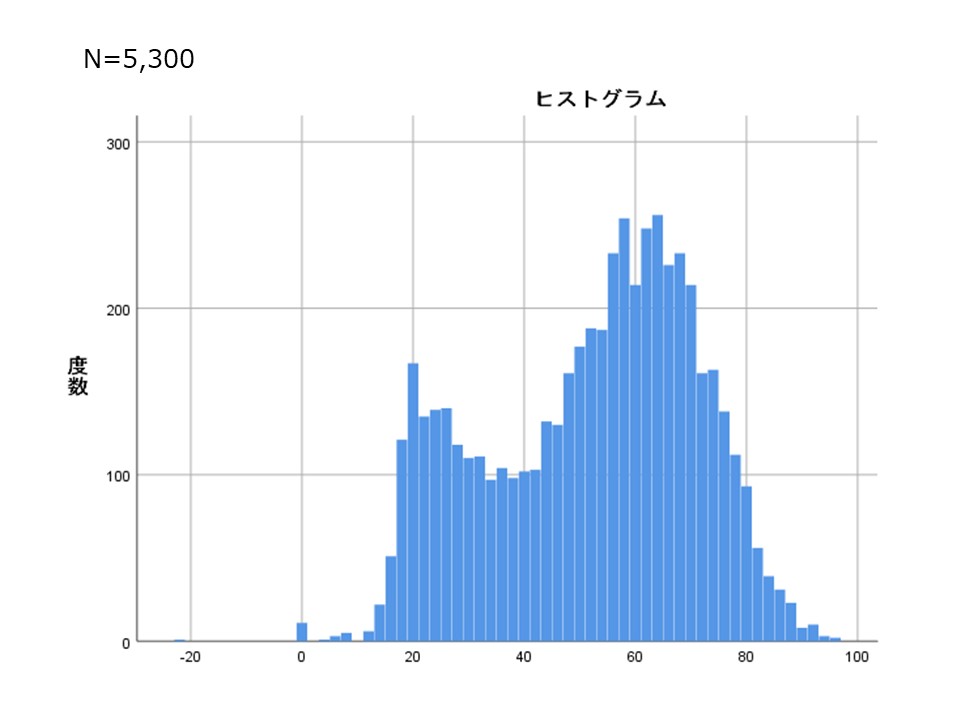
ヒストグラムの観察だけで正規分布を判断するのは難しい。
上の図のヒストグラムを視覚的に確認すると2峰性にみえる。
そのため正規分布していないようにみえる。
本当に正規分布していないのだろうか?
目で確認するだけでなく、ここでも統計ソフトを使用して検定を行う必要がある。
正規分布しているかどうかは統計ソフトを使用して検定を行う
正規分布の判断には、Shapiro-Wilk(シャピロ–ウィルク)検定を行うことが多い。
この検定では、検定によって正規分布か否かを判断する。
3例以上あれば検定可能と言われている。
※データが5,000以上の場合 ⇒ Kalmogorov-Smirnov(コルモゴロフ–スミルノフ)検定を行う。
検定結果の読み取り
・p<0.05の場合、「正規分布である」→パラメトリック
・p≧0.05の場合、「正規分布しない」→ノンパラメトリック
中心極限定理とは?
母集団の分布に関わらず、母集団から抽出された標本の数が十分に多い場合、標本平均の分布は正規分布に従う
「多くのデータが正規分布に従う」というだけでなく、仮に元のデータが正規分布に従ってなかったとしても、「そのデータの値をいくつか足しあわせたもの」はたいてい正規分布に収束する
世の中のたいていの確率現象は正規分布になると考えられている。
これを中心極限定理と言います。
正規分布まとめ
- 集めたデータがどの分析を行えるかを決めるためには必要な知識である。
- 多くのデータが正規分布に従うという性質を持つ。
- 正規分布しているかどうかは観察だけでは難しく、検定を行うことが必要である。









